In recent months, I’ve been exploring procedural level generation techniques and algorithms to streamline the level design process for my future game projects so that I can spend more time on gameplay programming. While I haven’t delved into some of the more advanced stuff, I think I gained enough experience to quickly create levels suitable for various genres. In this post, I will talk about my progress in incorporating procedural map generation into a MOBA game I’ve been working on (in Unity).

When approaching the level design task, it would make sense to start with a conceptual design, do some sketching and use generative AI to create inspirational visuals before moving on to the actual implementation. However, I chose to skip this part knowing that once I decided on the strategies and assembled my toolkit, procedural generation would give me satisfactory results in no time, and instead of drawings I would have a 3D scene to work with and build upon. In the case of a MOBA, there are only a few special areas and structures which can easily be integrated into the level generation process without requiring human intervention.

The first thing my level needed was a terrain whose shape looked natural and organic. While Unity’s built-in terrain features allow us to create and update terrains at runtime, I wanted more control over the generation process, so I decided not to use those features. One of the reasons behind this decision was my desire to stay away from grid based implementations as grids are not that interesting. However, grids are easy to work with, and now I needed more advanced algorithms to create points in 3D space and connect (triangulate) them to form surfaces. I knew that Poisson Disk Sampling would create nicely distributed point samples and Delaunay Triangulation would be able to triangulate these samples, which would give me the required data to create a Mesh.

My initial idea was to implement both of these algorithms myself so I could better understand how they worked. And I was able to implement the sampling algorithm which worked well. When I attempted to implement the triangulation algorithm, I realized that it would take a long time to do it and it would probably contain lots of bugs in it. I had implemented the Ear Clipping algorithm before (which wasn’t useful in this case), but this was much more complex. So I started looking for a C# implementation of Delaunay Triangulation and found this nice repository by Patryk Grech which also contained an implementation of the Poisson Disk Sampling algorithm. The sample scene in the project allowed me to learn how to use the code and confirm that it worked as expected.

The following code generates point samples inside a circular region, triangulates the points and creates a mesh by providing the required data to the mesh constructor.

var radius = 48f;
var minDistance = 1f;
var sampler = UniformPoissonDiskSampler.SampleCircle(center: Vector2.zero, radius: radius, minimumDistance: minDistance);
var points = sampler.ToPoints();
var delaunator = new Delaunator(points);
var vertices = new Vector3[delaunator.Points.Length];
for (var i = 0; i < points.Length; i++) {
  var x = (float)points[i].X;
  var z = (float)points[i].Y;
  // assign a noise (elevation) value to the y coordinate
  vertices[i] = new Vector3(x, y, z);
}
var mesh = new Mesh {vertices = vertices, triangles = delaunator.Triangles};
meshFilter.mesh = mesh;

The part below is what’s missing in the code above, which is the elevation calculation that utilizes Mathf.PerlinNoise. Getting good results for the terrain heights is all about finding good value ranges for the frequency, amplitude, octaves, persistence, lacunarity and offset parameters.

var amplitude = 3f;
var frequency = .04f;
var lacunarity = 2f;
var persistence = .5f;
var octaves = 4;
var y = 0f;
for (var j = 0; j < octaves; j++) {
  y += Mathf.PerlinNoise(x: offset + x * frequency, y: offset + z * frequency) * amplitude;
  frequency *= lacunarity;
  amplitude *= persistence;
}

By combining these two code blocks, I was able to create a mesh shaped like a terrain. But a mesh alone doesn’t make a terrain; it needed colors to visually indicate the differences in elevation. I wanted to give the terrain a low-poly look; so, I applied flat shading to faces in Shader Graph as described in this article by Hextant Studios. I picked five shades of ground/soil color and assigned them to individual vertices of the mesh based on elevation levels (each vertex falls into one of five levels). The following is the resulting terrain when viewed from above.

Procedurally generated terrain with elevation-based coloring

It looks natural enough, so I’m satisfied with the result. However, a barren land like this isn’t particularly interesting, so I decided to introduce obstacles (trees) into the terrain. In nature, trees don’t usually stand alone, instead they create formations. For this purpose, I could have set a threshold value and decided whether to place a tree at any point in the mesh by comparing its y value with the threshold. This approach would have resulted in tree covered areas that are above or below a certain height, resulting in unrealistic tree distributions. Instead, I decided to generate a distinct noise value for each point by adjusting the offset provided to PerlinNoise and re-running the algorithm. I stored the tree locations in a HashSet for later.

To place trees on the terrain I needed a tree mesh. I found what I was looking for in this package by Broken Vector. I knew that spawning many tree objects in a scene would result in significant performance issues, and I only wanted to display the trees with no extra functionality. As a result, I decided to use GPU instancing, which reduces the number of draw calls between the CPU and GPU, and improves performance when many instances of a mesh are being drawn. Even though the mesh is the same, it is still possible to apply a different transformation to each instance, which creates variation. So, I chose a tree model and passed it as a prefab to the MapContainer class which contains all the code related to map generation. I also created a shader for the trees that utilized the color sheets provided with the tree models.

[SerializeField] GameObject treePrefab;
[SerializeField] Material treeMaterial;
void Awake() {
  treeMesh = treePrefab.GetComponent<MeshFilter>().sharedMesh;
  treeParams = new RenderParams(mat: treeMaterial) {
    shadowCastingMode = UnityEngine.Rendering.ShadowCastingMode.On
  };
}

treeParams in the code above is an instance of the RenderParams class, which provides various parameters for rendering functions. Notice that the shadowCastingMode is set to on, which is required for instances to cast shadows even though the Cast Shadows option is enabled in the tree shader. In addition to the render parameters and the mesh to be rendered, the Graphics.RenderMeshInstanced method requires an array of Matrix4x4 that specifies the scale, rotation, and translation amounts for each instance. For variation, I randomized the scale and rotation of each tree within reasonable limits. Randomization calls are omitted in the following code.

treeData = new Matrix4x4[trees.Count];
var k = 0;
foreach (var pos in trees) {
  var translate = Matrix4x4.Translate(vector: pos);
  var scale = Matrix4x4.Scale(vector: new Vector3(scaleX, scaleY, scaleZ));
  var rotate = Matrix4x4.Rotate(q: Quaternion.Euler(rotateX, rotateY, rotateZ));
  var transform = translate * rotate * scale;
  treeData[k++] = transform;
}

After creating all the necessary data, it was time to make the render calls within the Update method so it would be executed every frame. If a mesh has multiple submeshes, calling RenderMeshInstanced is necessary for each submesh which can have their own set of parameters.

void Update () {
  if (treeData != null)
    Graphics.RenderMeshInstanced(rparams: treeParams, mesh: treeMesh, submeshIndex: 0, instanceData: treeData);
}

Tree formations created with Perlin Noise

With the addition of the trees, the map became more interesting and visually pleasing. However, it lacked a clear purpose since I hadn’t specified any regions of interest on the map. Now, it was time to introduce the first special regions into the map: the teams’ bases. Where to put the bases was obvious since the leading titles of the MOBA genre all follow the same rule: opposing ends of the diagonal from the bottom-left corner to the top-right corner. My terrain was centered around the xz-plane, so the first base would have negative x and z coordinates while the second one would be on the positive side of both axes. I had to decide on the base radius considering the distance between them and leave some margin from the borders of the terrain, as I wanted to cover the outer parts with trees to signify the boundaries of the map. Calculations of the center points of the bases are given below.

var sqrt2 = Mathf.Sqrt(f: 2);
var borderThickness = 4f;
var borderRadius = radius - borderThickness; // radius used in poisson disk sampling
var borderDistance = borderRadius / sqrt2; // divided by sqrt2 because of the angle (45 degrees) of the diagonal
var baseRadius = 2 * borderThickness;
var baseDistance = baseRadius / sqrt2;
var firstCenter = new Vector2(x: -borderDistance + baseDistance, y: -borderDistance + baseDistance);
var secondCenter = new Vector2(x: borderDistance - baseDistance, y: borderDistance - baseDistance);

When I ran the tree placement algorithm again with the same parameters multiple times while excluding the base areas, I occasionally obtained some decent maps but mostly, they were unplayable such as the following one.

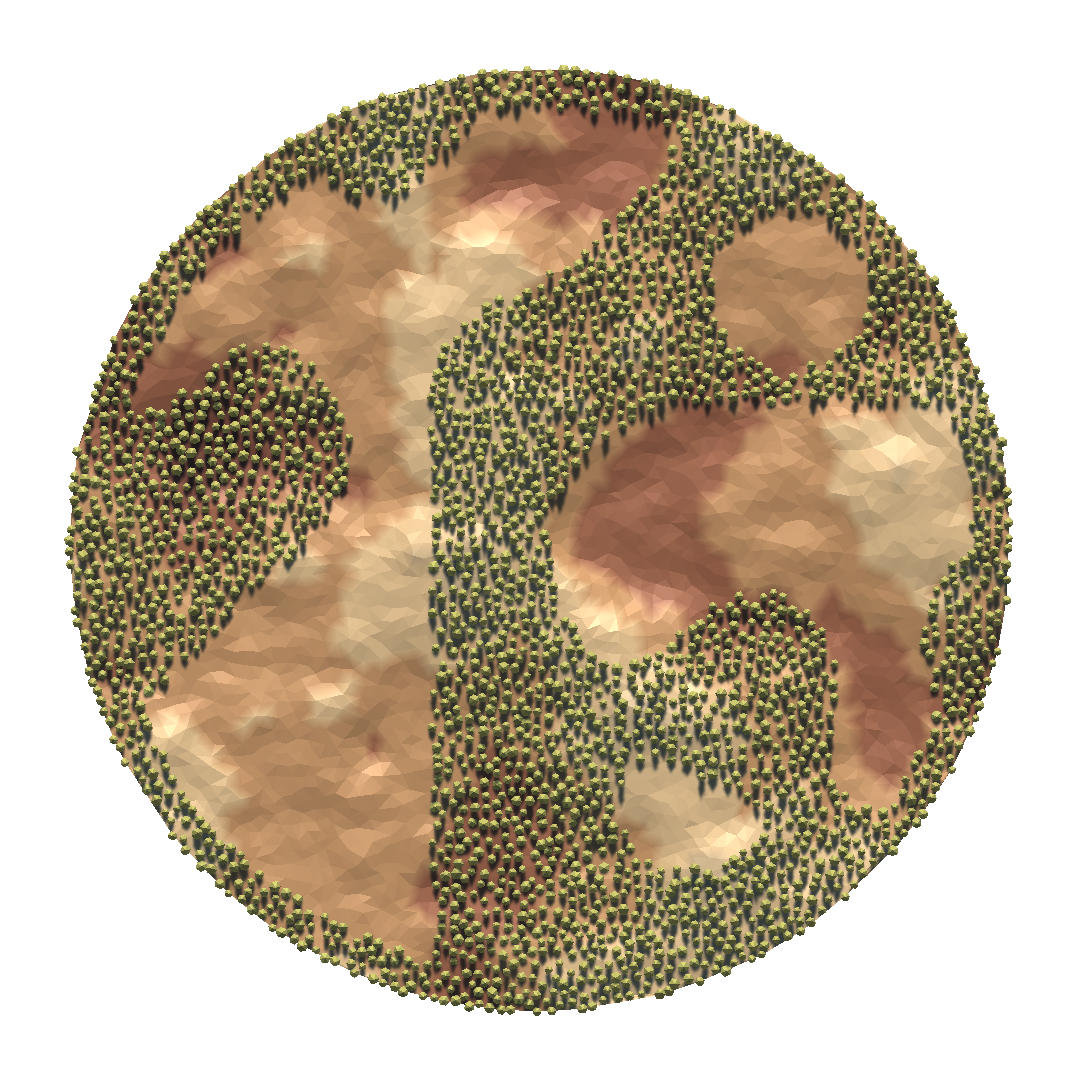
Map with disconnected regions

As you can see, the second base is fully covered by trees while the first one has access to only a small part of the map. I thought maybe I could get a better tree distribution by adjusting the parameters of the noise function. By increasing the frequency from .04 to .1, I got the following result.

More interesting map with disconnected regions

Even though there is a large enough connected walkable area, both bases are disconnected from it and there are many areas that cannot be reached. I figured that the tree density was too high to allow path formation between the bases. By changing the threshold value, which is compared against the noise value calculated at each vertex to determine whether to place a tree there, I started to see nice, almost fully-connected regions on the map. The only thing I did was to lower the tree density setting from .5 to .4, and I obtained the following map.

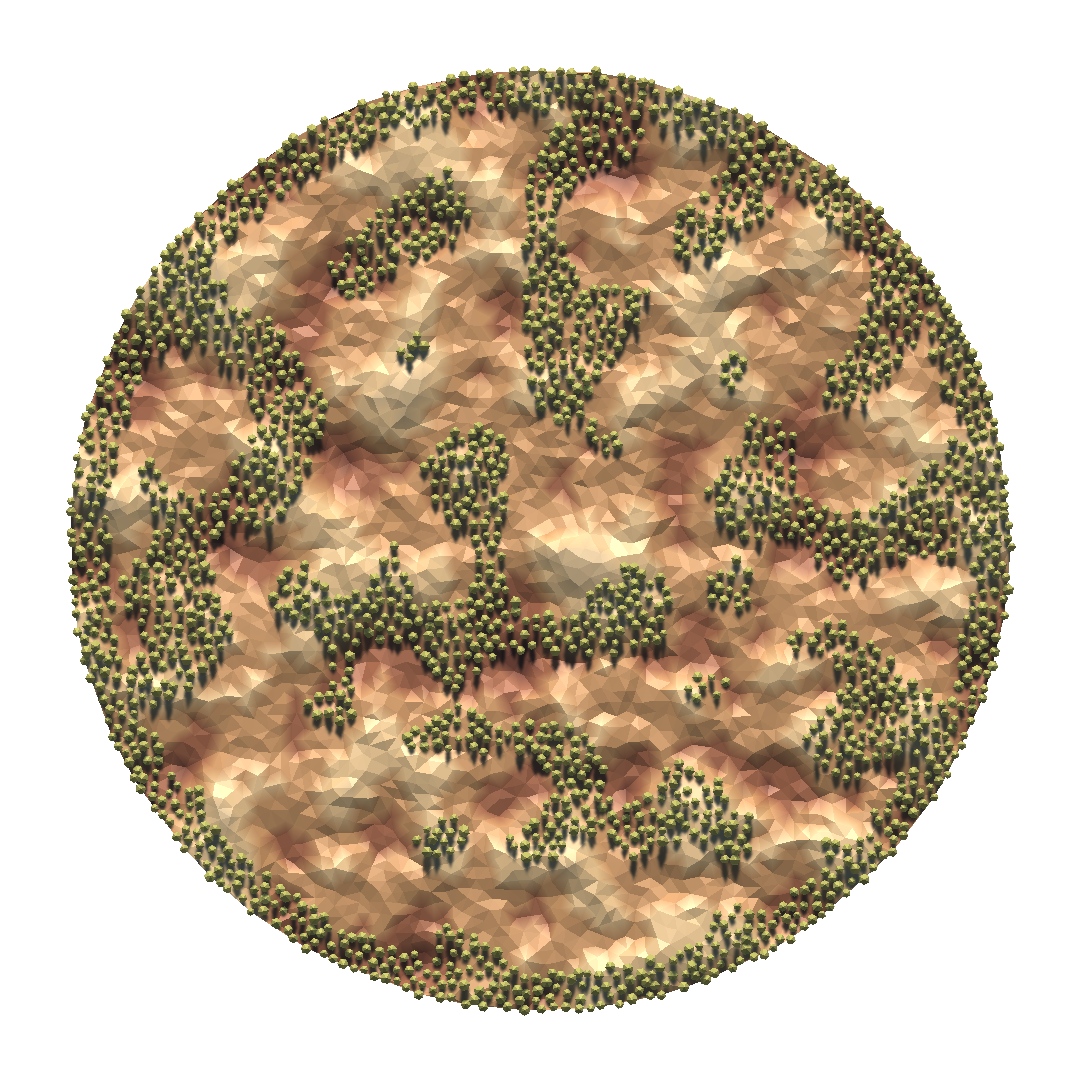
Map with mostly connected regions

However, I still saw cases where the bases were disconnected when I re-ran the algorithm. It was clear that no amount of micro-adjustments would guarantee an acceptable output unless I was willing to limit tree density to very low values. I thought I needed to give up on Perlin noise and started looking for another algorithm that could accomplish the task. I wanted something simple enough to implement but capable of producing complex results. Cellular automaton was what I was looking for, but I didn’t know which model to simulate. Since I was dealing with trees, I searched for known models involving trees. Then, I came across the forest-fire model.

The forest-fire model in the link above was implemented for grids, but it was applicable to arbitrary graphs as well. The model has four rules:

  • A burning tree dies (node becomes empty)
  • A tree starts burning if any of its neighbors are burning
  • A tree starts burning with some non-zero probability even if none of its neighbors are burning
  • An empty node can grow a tree with some non-zero probability

I quickly implemented the algorithm for my graph with initial tree placements determined by Perlin noise (there was no escaping from it). I ran the algorithm using the same parameter values from the article (tree probability: .05, fire probability: .001) for 10 iterations and created an animated GIF of the simulation.

Forest-fire simulation

I then ran this model a couple iterations on a map generated using the parameter values that resulted in nice outputs in earlier trials. However, I used a much higher initial fire probability (.1) compared to the simulation above (.001). See how it helps to connect the islands by breaking through the walls.

Forest-fire simulation with higher initial fire probability

Still not satisfied with the results, I began to explore mazes…